今回から、
といっても、
もっとも、
お題の説明と準備
本論に入る前に、
けれど、
今回採上げるベクトルの内積では、


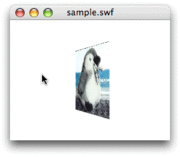
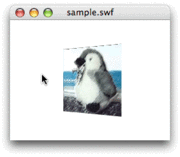
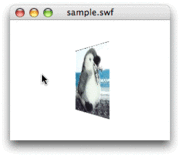
第48回スクリプト2は、
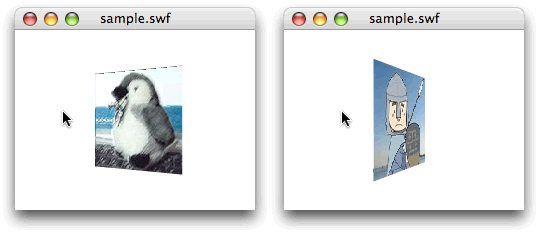
まず準備として、
![図2 [ライブラリ]に加えたビットマップに[クラス]を設定 図2 [ライブラリ]に加えたビットマップに[クラス]を設定](/assets/images/dev/serial/01/as3/0051/002.png)
ベクトルの内積から面の向きがわかる
ベクトルは方向をもった大きさで、
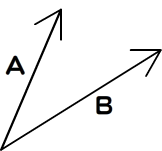
つまり、
3次元空間のベクトルを表すために、
| ベクトル | 座標 |
|---|---|
| 視線 | (0, 0, 1) |
| 面(初期値) | (0, 0, -1) |
そして、
| 面の向き | ふたつのベクトルのなす角 | 内積の符号 |
|---|---|---|
| 裏 | 90度より小さい | +(正) |
| 真横 | 90度 | 0 |
| 表 | 90度より大きい | -(負) |
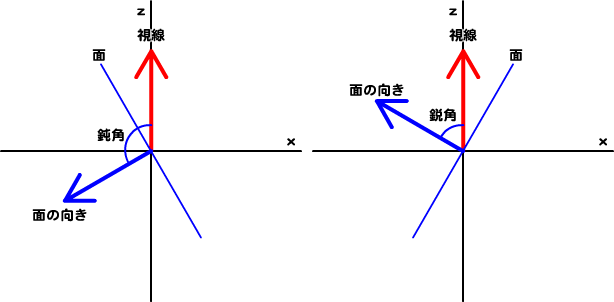
ここまでくれば、
- Vector3Dオブジェクト.dotProduct
(もうひとつのVector3Dオブジェクト)
面の表と裏を塗替える
では、
第2は、
今回3次元空間の頂点座標は動かさない。変換のMatrix3Dオブジェクトに回転を加えて、
その結果のオブジェクトを変数 (worldMatrix3D) に残す。つまり、 座標ではなく変換行列で座標変換を管理するのだ。
したがって、
// フレームアクションに追加
var viewVector3D:Vector3D = Vector3D.Z_AXIS; // 視線のベクトル
var faceVector3D:Vector3D = new Vector3D(0, 0, -1); // 面のベクトル
function xRotate(eventObject:Event):void {
var nRotationY:Number = mySprite.mouseX * nDeceleration;
var vertices2D:Vector.<Number> = new Vector.<Number>();
xTransform(vertices2D, nRotationY);
var bFront:Boolean = xIsFront(faceVector3D, worldMatrix3D); // 面の表裏を調べる
trace(bFront); // 確認用
xDraw(vertices2D);
}
// 面の表裏を調べる関数の定義
function xIsFront(myVector3D:Vector3D, myMatrix3D:Matrix3D):Boolean {
var directionVector3D:Vector3D = myMatrix3D.transformVector(myVector3D);
var bFront:Boolean = (viewVector3D.dotProduct(directionVector3D) < 0);
return bFront;
}面の表裏を調べる関数
![図5 関数の戻り値を[出力]するときフレームレートは落とした方が見やすい 図5 関数の戻り値を[出力]するときフレームレートは落とした方が見やすい](/assets/images/dev/serial/01/as3/0051/thumb/TH800_005.png)
それでは、
第2に、
そして第3に、
// フレームアクションに追加
var backTexture:BitmapData = new Image2(); // 追加
function xRotate(eventObject:Event):void {
var nRotationY:Number = mySprite.mouseX * nDeceleration;
var vertices2D:Vector.<Number> = new Vector.<Number>();
xTransform(vertices2D, nRotationY);
var bFront:Boolean = xIsFront(faceVector3D, worldMatrix3D);
// trace(bFront); // 確認用
// xDraw(vertices2D);
xDraw(vertices2D, bFront);
}
// function xDraw(vertices2D:Vector.<Number>):void {
function xDraw(vertices2D:Vector.<Number>, bFront:Boolean):void {
var texture:BitmapData = bFront ? myTexture : backTexture; // 追加
myGraphics.clear();
// myGraphics.beginBitmapFill(myTexture);
myGraphics.beginBitmapFill(texture);
myGraphics.drawTriangles(vertices2D, indices, uvtData);
myGraphics.endFill();
}修正し終えたフレームアクション全体を、
// フレームアクション
var nUnit:Number = 100 / 2;
var mySprite:Sprite = new Sprite();
var myTexture:BitmapData = new Image();
var backTexture:BitmapData = new Image2();
var viewVector3D:Vector3D = Vector3D.Z_AXIS;
var faceVector3D:Vector3D = new Vector3D(0, 0, -1);
var vertices:Vector.<Number> = new Vector.<Number>();
var indices:Vector.<int> = new Vector.<int>();
var uvtData:Vector.<Number> = new Vector.<Number>();
var nDeceleration:Number = 0.3;
var myGraphics:Graphics = mySprite.graphics;
var myPerspective:PerspectiveProjection = transform.perspectiveProjection;
var worldMatrix3D:Matrix3D = new Matrix3D();
var viewMatrix3D:Matrix3D = myPerspective.toMatrix3D();
viewMatrix3D.prependTranslation(0, 0, myPerspective.focalLength);
mySprite.x = stage.stageWidth / 2;
mySprite.y = stage.stageHeight / 2;
vertices.push(-nUnit, -nUnit, 0);
vertices.push(nUnit, -nUnit, 0);
vertices.push(nUnit, nUnit, 0);
vertices.push(-nUnit, nUnit, 0);
indices.push(0, 1, 3);
indices.push(1, 2, 3);
uvtData.push(0, 0, 0);
uvtData.push(1, 0, 0);
uvtData.push(1, 1, 0);
uvtData.push(0, 1, 0);
addChild(mySprite);
addEventListener(Event.ENTER_FRAME, xRotate);
function xRotate(eventObject:Event):void {
var nRotationY:Number = mySprite.mouseX * nDeceleration;
var vertices2D:Vector.<Number> = new Vector.<Number>();
xTransform(vertices2D, nRotationY);
var bFront:Boolean = xIsFront(faceVector3D, worldMatrix3D);
xDraw(vertices2D, bFront);
}
function xTransform(vertices2D:Vector.<Number>, myRotation:Number):void {
worldMatrix3D.prependRotation(myRotation, Vector3D.Y_AXIS);
var myMatrix3D:Matrix3D = worldMatrix3D.clone();
myMatrix3D.append(viewMatrix3D);
Utils3D.projectVectors(myMatrix3D, vertices, vertices2D, uvtData);
}
function xDraw(vertices2D:Vector.<Number>, bFront:Boolean):void {
var texture:BitmapData = bFront ? myTexture : backTexture;
myGraphics.clear();
myGraphics.beginBitmapFill(texture);
myGraphics.drawTriangles(vertices2D, indices, uvtData);
myGraphics.endFill();
}
function xIsFront(myVector3D:Vector3D, myMatrix3D:Matrix3D):Boolean {
var directionVector3D:Vector3D = myMatrix3D.transformVector(myVector3D);
var bFront:Boolean = (viewVector3D.dotProduct(directionVector3D) < 0);
return bFront;
}ベクトルの内積を数学的に理解する
ベクトルの内積について、
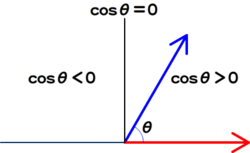
ベクトルAとBの内積は、
A・
B = |A||B|cosθ A||B| > 0 (|A|≠0、
|B|≠0とする) A・
B = axbx + ayby A・
B = axbx + ayby + azbz - スクリプト1のサンプルファイル
(CS5形式/約61KB)
ベクトルAとBの始点を結んだとき、
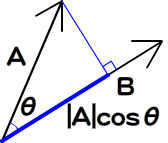
ベクトルAとBの絶対値は、
つまり、
内積は、
3次元空間のベクトルA
次回は、
今回解説した次のサンプルファイルがダウンロードできます。