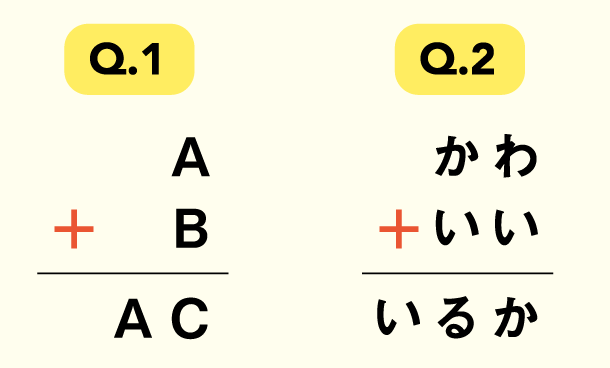
覆面算を解く
覆面算とは、ひらがなやアルファベットに置き換えられた筆算を、次のルールで数字の筆算に復元するパズルです。
- 同じ文字には同じ数字が入る
- 異なる文字には異なる数字が入る
- 左端の文字には0が入らない
覆面算を解くアルゴリズムとして最も簡単なのは、各文字に数字を当てはめる方法をすべて調べる「力まかせ探索」でしょう。しかし、より高速手法があります。覆面算を「文字に数字を入れていく途中経過」が頂点、「文字に数字を入れる操作」が辺であるグラフとみなして、深さ優先探索を行う方法です。
まず、覆面算全体の0行めの単語の一の位の文字に対して、0~9までの数字を順に試します。次に、それぞれの場合について、1行めの単語の一の位にさきほど入れた数字以外を順に試します。これを繰り返すことで、最終的に正しい筆算式を求めることができるのです。たとえばQ.2は、次のように探索します(Q.1はただの1桁の足し算ですので、答えを省略します)。
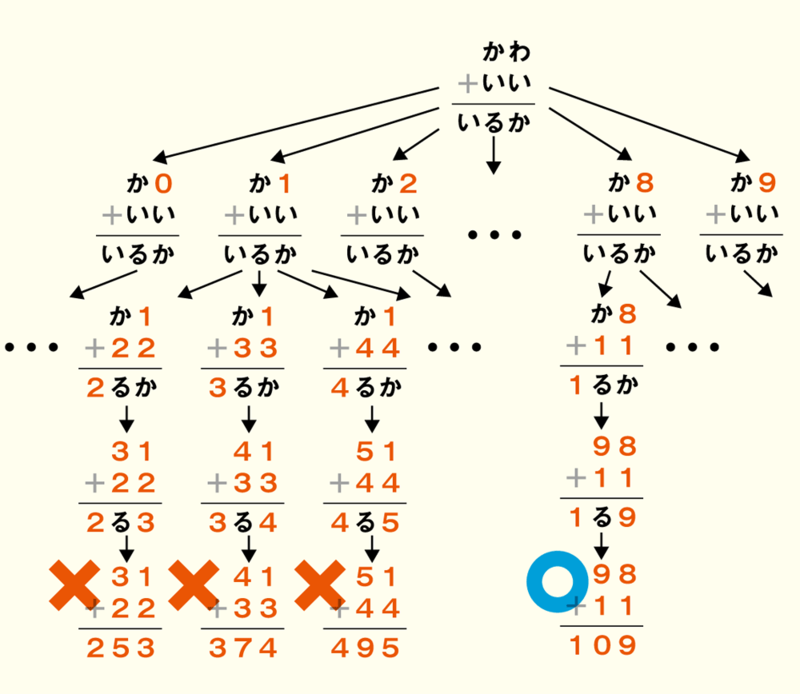
なお、すべての文字に数字を入れ終えていなくても、その時点で矛盾が見つかれば探索を打ち切る枝刈りを行うことで、さらに探索を効率化できます。
迷路の最短経路を求める
迷路は、与えられた地図上の複雑に入り組んだ道を抜けて、ゴールまでたどり着くことを目指す図形パズルの一種です。今回は、次のようなマス目で区切られた地図において、スタート(S)からゴール(G)へと至る最短経路を考えてみます。
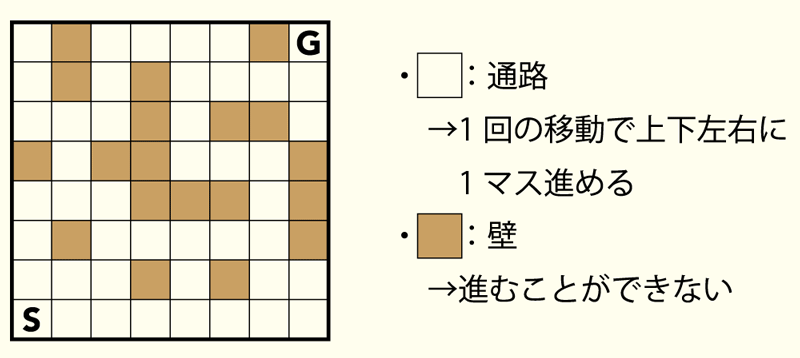
迷路の最短経路は幅優先探索という探索アルゴリズムによって求めることができます。出発点に近いところから順に探索する方法です。
スタートマスから1手で行けるマスに「1」を、続いて「1」のマスから1手で行けるマスに「2」を、……と書き込んでいきます。この幅優先探索の過程では、一度数字を書き込んだマスの数値は更新しないことに注意しましょう。数値が書き込まれた瞬間に、その手前のマスへと矢印をひきます。この矢印をたどることで、スタートからゴールへと至る最短経路が得られます。このような手続きを経路復元と呼びます。
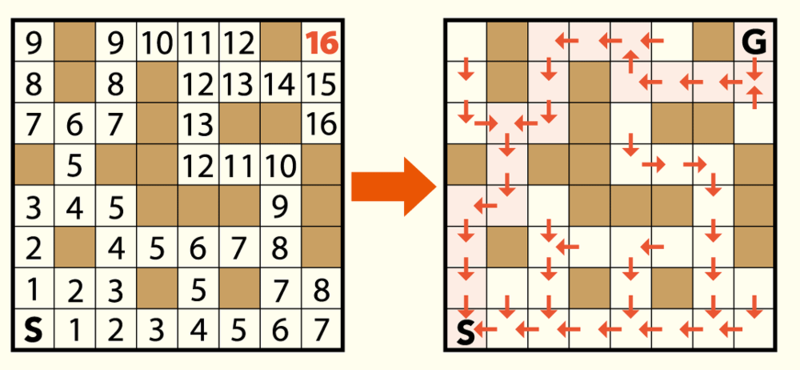
そしてこの迷路は、各マスを頂点とし、マスとマスとの隣接関係を辺としたグラフとみなせます。グラフ上の幅優先探索とみなすことで、より汎用的に使えるようになります。
書籍『パズルで鍛えるアルゴリズム力』では、パズルを解く方法を考察し、答えを出力する「ソルバー」を実装することで、アルゴリズムを考える力を鍛えます。ここでは2つのパズルについて、探索アルゴリズムによる解法を紹介しましたが、さまざまなパズルとアルゴリズムを紹介していますので、興味のある方はぜひ手に取ってみてください。







