概要
本書は,物理シミュレーションについて学びたい方々のために書かれた,PythonとVPythonの解説書です。Pythonは,学習しやすさに加え,様々な目的のために利用できるライブラリが豊富に用意されていることから,近年人気の高いプログラミング言語の一つとなっています。また,VPythonは,3次元のグラフィックスやアニメーションを作成するための,Pythonのライブラリです。Pythonに加え,VPythonの基本的な使い方を学習すれば,動画サイト等で紹介されているレベルの物理シミュレーション動画を,比較的短時間で作成できるようになるでしょう。
こんな方におすすめ
- Pythonによる物理シミュレーションを卒業研究のテーマにしたい大学生
- シミュレーション結果をグラフやアニメーションにし,プレゼン資料を作成したい大学院生
- 趣味で物理シミュレーションの動画を作ってみたい社会人
- 「情報I」の授業内容の理解を深め,発展させたい高校生
目次
第1章 VPythonをはじめよう
- 1.1 VPythonとは何だろう?
- 1.2 本書の目的
- 1.3 本書の構成
- 1.4 サンプルプログラムを動かしてみよう
第2章 プログラミング環境を整えよう
- 2.1 プログラミング環境の構築
- 2.2 Jupyter Notebookの起動と基本操作
第3章 Pythonの基本文法
- 3.1 四則演算
- 3.2 変数を使う計算
- 3.3 コメントの入力
- 3.4 複数の命令文を1行で書く
- 3.5 データの型
- 3.6 関数
- 3.7 メソッド
- 3.8 モジュール
- 3.9 繰り返し操作
- 3.10 条件文
- 3.11 関数の定義とモジュールの作成
- 3.12 ファイルの入出力
- 3.13 練習問題
第4章 VPythonのプログラムを書いてみよう
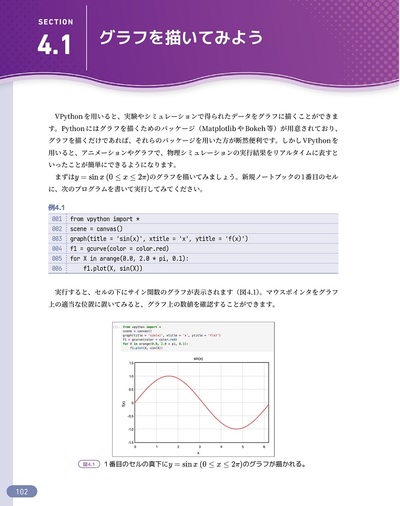
- 4.1 グラフを描いてみよう
- 4.2 オブジェクトを描いてみよう
第5章 物理シミュレーションの基礎
- 5.1 ベクトルの計算
- 5.2 オイラー法による微分方程式の数値解法
- 5.3 ルンゲ・クッタ法による一階微分方程式の数値解法
- 5.4 ルンゲ・クッタ法による二階微分方程式の数値解法
- 5.5 計算結果をアニメーションで可視化する方法
第6章 いろいろな物理シミュレーション
- 6.1 ランダムウォーク
- 6.2 二重振り子
- 6.3 天体の運動
- 6.4 ベクトル場の可視化
- 6.5 分子動力学シミュレーション
- 付録A 色の指定
- 付録B Web VPythonの使い方
- 付録C トラブルシューティング
- 付録D さらに勉強したい人のための文献リスト
- 参考文献
サポート
ダウンロード
書籍で使用しているコードは以下よりダウンロードできます。
(2024年10月21日更新)
- ダウンロード
- VPythonBook.zip
正誤表
本書の以下の部分に誤りがありました。ここに訂正するとともに,ご迷惑をおかけしたことを深くお詫び申し上げます。
第1刷
P.105 本文上から2行目のコード行
| 誤 |
... xtitle = 'x', ytitle = 'f(x)', fast = True)
|
|---|
| 正 |
... xtitle = 'x', ytitle = 'f(x)', fast = False)
|
|---|
P.145 例4.30のプログラムコード002行目
| 誤 |
|
|---|
| 正 |
今の「ball = sphere()」の前に「scene = canvas()」を1行挿入(別のセルの出力結果に上書きされないように) |
|---|
P.146 例4.31のプログラムコード002行目
| 誤 |
|
|---|
| 正 |
今の「ball = sphere()」の前に「scene = canvas()」を1行挿入(別のセルの出力結果に上書きされないように) |
|---|
P.175 本文下から3行目
| 誤 |
…、ルンゲ・クッタ法を用いました。 |
|---|
| 正 |
…、オイラー法を用いました。 |
|---|