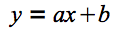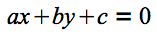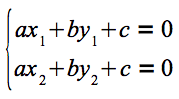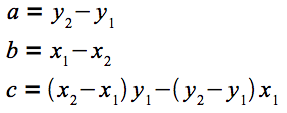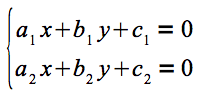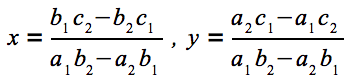計算幾何学とは
小学生や中学生の頃、算数や数学の授業で、台形の面積を求めたり、直線の方程式を解いたりした記憶が誰にでもあることでしょう。計算幾何学とは、コンピュータサイエンスの立場から、こうした「図形」に関するアルゴリズムを研究する学問です。計算幾何学は、今日のコンピュータグラフィックスやCADの発展においてきわめて重要な役割を担っているほか、地理情報システム(GIS)やロボット工学といった数多くの分野に応用されています。
本連載では、ブログ可視化サイトの「Blogopolis」で採用されている計算幾何的アプローチを引き合いに出しつつ、Javaプログラムでアルゴリズムを実装しながら、計算幾何学の初歩を学びます。
Blogopolisとボロノイ図
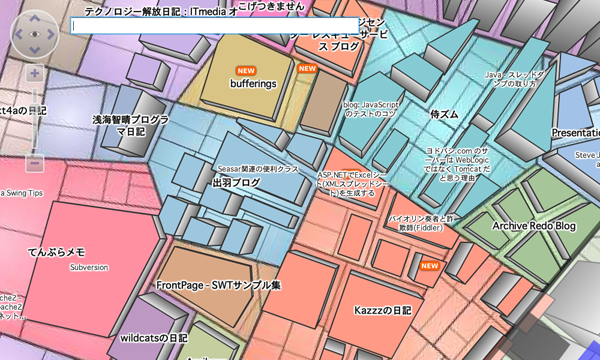
Blogopolis は筆者の開発したWebサイトで、主に日本国内で開設された25万件以上のブログを解析し、「 仮想都市景観」として視覚化したサービスです。Blogopolisでは、1人1人のブロガーが人気度に応じた広さの「土地」を持っています。土地の中では、ブログの個別記事を示す「ビル」が立ち並び、オフィス街のような見た目を形成しています。
図1 BlogopolisBlogopolisの外観は3Dですが、その3D表現の基盤になっているのは、2次元平面上の区画分けアルゴリズムです。この区画分けには、ボロノイ図(voronoi diagram)をアレンジした手法が使われています。
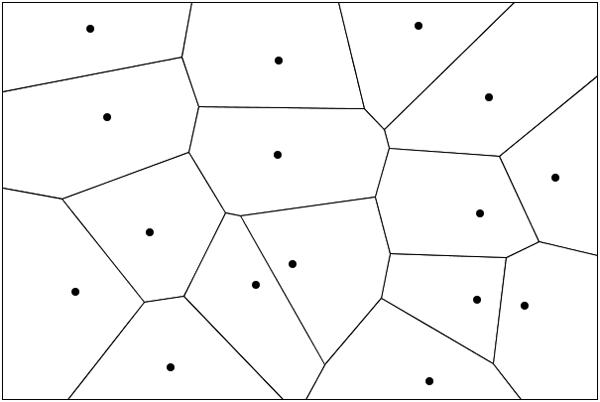
ボロノイ図は、複数個の母点との距離にもとづいて領域を分割した図で、計算幾何学の重要なテーマの1つです。もっとも単純なボロノイ図では、「 どの母点との距離が最短になるか」によって分割が決定されて境界線が引かれるため、境界線は2つの母点の垂直二等分線になっています。
図2 ボロノイ図ボロノイ図はさまざまな応用ができますが、その1つに商圏分析があります。例えば図2で、各母点の位置にコンビニエンスストアが建っているとしましょう。客は自宅から最も近いコンビニエンスストアに行くと仮定した場合、各店舗が集客を見込めるエリアは、ボロノイ図で分割された領域で推定することができます。
幾何ライブラリ
多くのプログラミング言語では、幾何が標準ライブラリでサポートされていたり、外部ライブラリとして提供されています。例えばJavaでは、java.awt.geomパッケージ以下のクラスを使って、基本図形の定義や交差判定、パスの結合といった操作を行うことができます。
こうしたライブラリは高度に抽象化されており、内部実装を知らなくても簡単に利用できます。図形を扱う大半の用途では、標準のライブラリを呼び出すだけで事足りるはずです。しかし、より複雑な問題を解く場合には、それぞれの問題に適したデータ構造やアルゴリズムを独自に実装する必要も出てきます。いずれにせよ、計算幾何の基本的な考え方を知り、動作原理に触れておくことは有益でしょう。
本連載のロードマップ
本連載では、計算幾何学の中でも特に基本的な内容として、直線、線分、そして多角形を取り上げます。初めに、2次元平面上で直線と線分を表現するクラスを作成し、それらが交差する条件を調べます。次に、平面走査法(plane sweep algorithm)と呼ばれるアルゴリズムを使って、多数の線分の中から交差点を高速に検出する方法を学びます。さらに、線分を組み合わせて多角形を表現し、多角形を使った演算について見ていきます。最後に、これまで学んだ手法を組み合わせ、ボロノイ図の作成に挑戦します。
Javaの開発環境について
本連載では、プログラミング言語としてJavaを使用します。手元にJavaの開発環境がなく、本連載のプログラムを試したい場合には、 NetBeans の導入をおすすめします。NetBeansはオールインワン型のIDEですので、インストールするだけで特別な設定の必要もなく、一通りの開発環境を整えることができます。
直線クラスの作成
まず、中学数学の復習から始めましょう。2次元平面上の直線は、どのような式で表すことができるでしょうか。
図3 2次元平面上の数値を表す数式(その1) 上の式を思い浮かべた人が多いかもしれません。aは直線の傾き、bはy軸の切片です。しかし、この式ではy軸に平行な直線を表現できないため、以下の一般形を使うのが正解になります。
図4 2次元平面上の数値を表す数式(その2、こちらが正解) a、b、cの3つのパラメータがあれば、2次元平面上の任意の直線を示せるのです。ではこれを、Lineクラスとして作成してみましょう。
Javaによる2次元平面上の任意の直線
public class Line {
public double a;
public double b;
public double c;
public Line(double a, double b, double c) {
this.a = a;
this.b = b;
this.c = c;
}
@Override
public String toString() {
return "a = " + a + ", b = " + b + ", c = " + c;
}
}簡略化のため、a、b、cはpublicフィールドとして宣言し、getterやsetterのメソッドは設けていません。また、デバッグを容易にするため、toString()メソッドをオーバーライドしています。
2点を通る直線のパラメータ
さて、このLineクラスのインスタンスを作成するとき、2点の異なる座標(x1 , y1 )と(x2 , y2 )を与えて、その2点を通る直線を示すようにパラメータの値を決定できれば便利です。
このa、b、cを求めてみましょう。
直線の式に(x1 , y1 )と(x2 , y2 )を代入すると、以下の連立一次方程式が得られます。
図5 連立一次方程式この方程式を解くと、a、b、cは次のように決定します。
図6 前述の方程式を解いたところそれではこの解を使って、Lineクラスに、直線を通る2点の座標からインスタンスを作成するファクトリメソッドfromPoints()を追加してみましょう。
Javaによる連立一次方程式
public static Line fromPoints(double x1, double y1, double x2, double y2) {
double dx = x2 - x1;
double dy = y2 - y1;
return new Line(dy, -dx, dx * y1 - dy * x1);
}2直線の交点
平行でない2つの直線は、必ず1点で交わります。この交点座標を求めてみましょう。Lineクラスの2つのインスタンスl1とl2について、l1のa、b、cの各パラメータを(a1 , b1 , c1 )、l2のパラメータを(a2 , b2 , c2 )とします。このとき、l1とl2の交点を(x, y)とすると、以下の連立一次方程式が成立します。
図7 連立一次方程式(その2) この方程式を解くと、x, yは次のように決定します。
図8 前述の方程式を解いたところxとyの分母は共通ですが、2直線が平行のとき、この分母は0になります。
以上をふまえて、他の直線との交点座標を返すメソッドgetIntersectionPoint()をLineクラスに追加してみます。
Javaによる連立一次方程式(その1)
public Point2D getIntersectionPoint(Line l) {
double d = a * l.b - l.a * b;
if (d == 0.0) {
return null; // 直線が平行の場合はnullを返す
}
double x = (b * l.c - l.b * c) / d;
double y = (l.a * c - a * l.c) / d;
return new Point2D.Double(x, y);
}動作確認
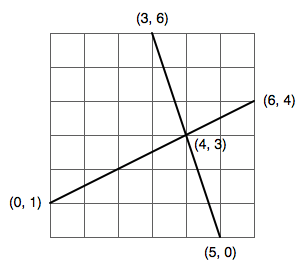
それでは、getIntersectionPoint()メソッドが正しく動作するか検証してみましょう。次の図に示す2直線は、座標(4, 3)で交わるはずです。
図9 2直線の交点以下のテストプログラムで、これを確認してみます。
Javaによる2直線の交点の出力
public class LineDemo {
public static void main(String[] args) {
Line l1 = Line.fromPoints(0, 1, 6, 4);
Line l2 = Line.fromPoints(3, 6, 5, 0);
Point2D p = l1.getIntersectionPoint(l2);
System.out.println("intersection = " + p);
}
}プログラムを実行すると、次の出力が得られます。
プログラムの実行
intersection = Point2D.Double[4.0, 3.0]想定通り、交点が正しく求められることを確認できました。
まとめと次回予告
今回は、計算幾何学の概要を説明し、Blogopolisで使用しているボロノイ図を紹介しました。また、計算幾何を実践的に学ぶための準備段階として、2次元平面上の直線を表現するLineクラスをJavaで作成し、2直線の交点座標を求めるメソッドを実装しました。
今回作成したプログラムのソースコードがダウンロードできます。
次回は、今回の内容にもとづいて2点を結ぶ線分クラスを作成し、線分の交差判定について考えていきます。お楽しみに!