2月も下旬になると暖かい日が増えてきました。新型コロナ対策の緊急事態宣言は続いているものの、そのような人間の営みとは無関係に、季節は着実に進んでいます。

さて前回は、提供割合「1％」のガチャを何回くらい回せば目的のキャラが手に入るかを、確率とシミュレーションを使って考えました。その結果、「⁠4割弱の人は100回引いても当たらない」一方、クジ運がいい順に参加者を並べてみると、「⁠全体の1/4は30回程度、半数は70回程度、3/4は140回程度で当たる一方、残りの1/4の人は140回以上かかる」ということがわかりました。

この種の結果は、数字だけで示すよりグラフ等を添えると理解が深まります。Pythonには簡単にグラフを描くことのできるmatplotlibという便利なツール（モジュール）があるので、今回はこのmatplotlibを紹介しつつ、前回の結果をグラフ化してみましょう。

matplotlibの使い方

matplotlibはPythonのパッケージコレクションPyPI（Python Package Index）に登録されているので、簡単にインストールできます。

$ python -m pip install -U matplotlib
Defaulting to user installation because normal site-packages is not writeable
Collecting matplotlib
  Downloading matplotlib-3.3.4-cp39-cp39-manylinux1_x86_64.whl (11.5 MB)
     |████████████████████████████████| 11.5 MB 10.3 MB/s 
Requirement already satisfied: pillow>=6.2.0 in /usr/lib/python3.9/site-packages (from matplotlib) (8.1.0)
....
  Downloading kiwisolver-1.3.1-cp39-cp39-manylinux1_x86_64.whl (1.2 MB)
     |████████████████████████████████| 1.2 MB 29.9 MB/s 
Requirement already satisfied: six in /usr/lib/python3.9/site-packages (from cycler>=0.10->matplotlib) (1.15.0)
Installing collected packages: python-dateutil, kiwisolver, cycler, matplotlib
Successfully installed cycler-0.10.0 kiwisolver-1.3.1 matplotlib-3.3.4 python-dateutil-2.8.1

この例では一般ユーザ権限でインストールしたので、そのユーザのホームディレクトリの.local/以下にパッケージがインストールされます。

$ ls ~/.local/lib/python3.9/site-packages/
__pycache__/                                matplotlib/
cycler-0.10.0.dist-info/                    matplotlib-3.3.4-py3.9-nspkg.pth
cycler.py                                   matplotlib-3.3.4.dist-info/
dateutil/                                   mpl_toolkits/
kiwisolver-1.3.1.dist-info/                 pylab.py
kiwisolver.cpython-39-x86_64-linux-gnu.so*  python_dateutil-2.8.1.dist-info/

上記コマンドをルート権限で実行すれば/usr/lib/python3.9/site-packages/以下にインストールされ、システム全体で利用可能になります。

matplotlibにはさまざまな機能があるものの、今回はpyplotと呼ばれるグラフ描画機能を試してみます。まずPythonを起動し、matplotlibからpyplotモジュールをimportします。

$ python
Python 3.9.1 (default, Jan 24 2021, 16:05:20) 
[GCC 10.2.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> from matplotlib import pyplot

次に適当なX,Yのデータを用意し、折れ線グラフを書くメソッドpyplot.plot()に渡します。

>>> x = [1,2,3,4]
>>> y = [10,30,50,20]
>>> pyplot.plot(x,y)
[<matplotlib.lines.Line2D object at 0x7fe290071580>]

描いたグラフを表示するメソッドpyplot.show()で作成されたグラフを描画します。

>>> pyplot.show()

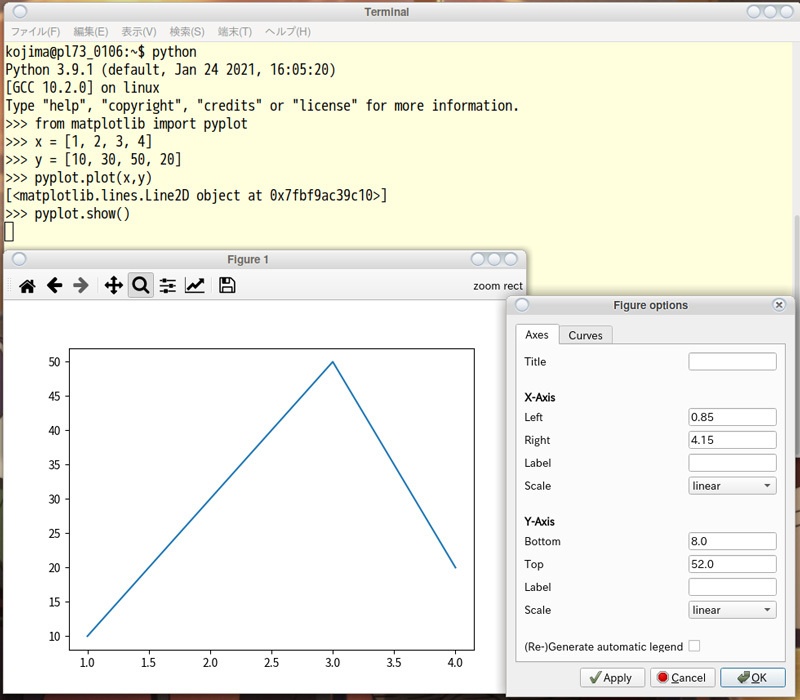
このように、グラフ化したいデータを渡すだけで、後はmatplotlibが自動的にグラフを作成してくれます。独立したウィンドウに描かれたグラフは、マウス操作で拡大縮小したり、軸のラベルを付けたり、線の種類や色、各ポイントのマーカーの有無や種類等を変更できます。また、これらの設定はpyplot.plot()へ渡すオプションとしても指定できるので、かなり凝ったグラフを作ることもできます。

ガチャ確率のグラフ化

さて、それでは前回の結果をmatplotlibでグラフ化するため、先のスクリプトを少し改造してみましょう。22行目はhist[]の各データに対するX軸の値で、それぞれ"10回以内"、"20回以内"……"100回以上"を意味します。また、今回は棒グラフで描くためのメソッドpyplot.bar()を使ってみます。

 1  import random
 2  from matplotlib import pyplot
 3  
 4  rate = 0.01
 5  player = 1000
 6  counter = []
 7  
 8  for i in range(player) :
 9      c = 1  
10      while random.random() > rate :
11          c += 1
12      counter.append(c)
13  
14  hist = [0,0,0,0,0,0,0,0,0,0,0]
15  for i in counter:
16      gr = int((i-1) / 10)
17      if gr > 10 :
18          hist[10] += 1
19      else:
20          hist[gr] += 1
21  
22  x = [10,20,30,40,50,60,70,80,90,100,110]
23  
24  pyplot.bar(x,hist)
25  pyplot.show()

このスクリプトを走らせると、こんなグラフになりました。

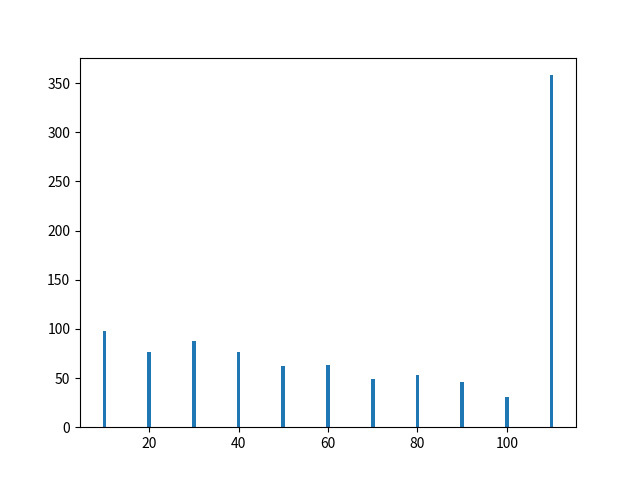
matplotlibで描かれたグラフは、マウスカーソルをあてると座標の数字を読み取れるので、ざっと確認したところ、10回以内で当たった人は98人、その後20回以内に当たった人は76人、30回以内に当たった人は88人……で、100回引いても当たらなかった人は360人、という結果になっていました。

先のスクリプトでは度数分布を自前で計算したものの、matplotlibにはpyplot.hist()という、度数分布（ヒストグラム）を自動的に計算してグラフ化する機能も用意されています。これを使えばスクリプトはずっと簡単になります。

 1  import random
 2  from matplotlib import pyplot
 3  
 4  rate = 0.01
 5  player = 1000
 6  counter = []
 7  
 8  for i in range(player) :
 9      c = 1  
10      while random.random() > rate :
11          c += 1
12      counter.append(c)
13  
14  pyplot.hist(counter)
15  pyplot.show()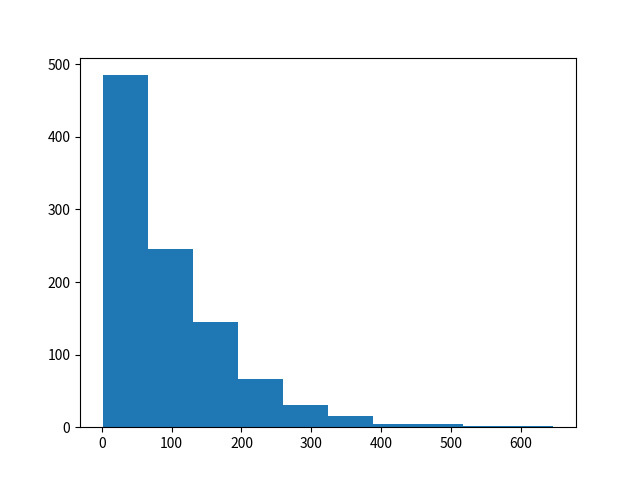

pyplot.hist()では、指定しないと柱（bins）の数が10になるように階級（グループ）が作られるので、かなり大まかな形状になりました。もう少し細かく見るため、柱の数を100にしてみます。

14  pyplot.hist(counter, bins=100)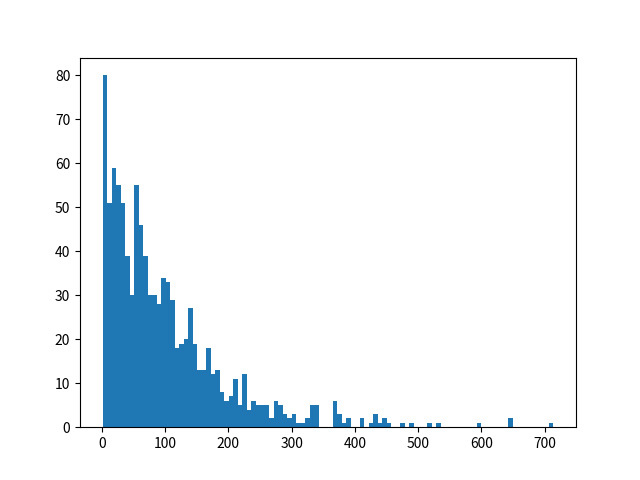

この結果を見ると、乱数を使ったシミュレーションのためかなりデコボコしているものの、急速に減少していく右肩下りな一方、裾野は長く延び、一番運の悪い人は700回以上回していることがわかります。

pyplot.hist()はcumulative=Trueを指定して累積を表示させることもできます。累積表示の場合、棒グラフのままだと画面が埋まってしまって見づらいので、histtype='step'も指定して、棒グラフの輪郭線のみを表示するようにしてみます。ついでに、前回紹介した四分位数のところに赤い点線を引いてみましょう。

14  pyplot.hist(counter, bins=100, cumulative=True, histtype='step')
15  pyplot.axhline(int(player/4),ls='--',c='red')
16  pyplot.axhline(int(player/2), ls='--', c='red')
17  pyplot.axhline(int(player - player/4), ls='--', c='red')
18  pyplot.show()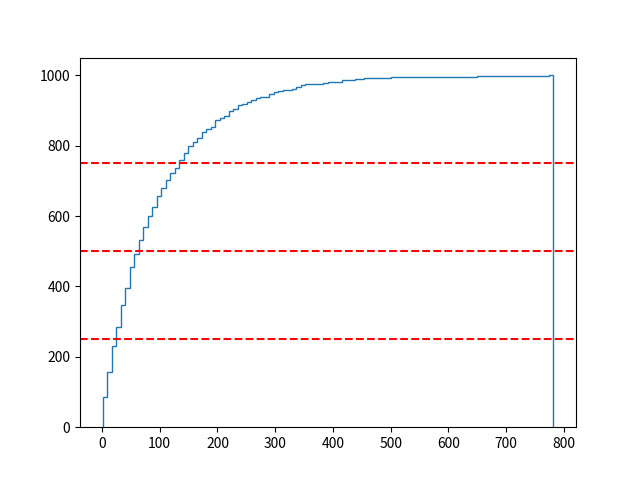

このグラフは一見、800の手前で急降下している折れ線グラフのように見えるものの、本来は棒グラフの輪郭になっていて、一番運の悪かった人が782回目に当たってグラフが1000人に逹したことを示しています。また、赤い点線との交点を調べると、250番目の人は25回目、500番目の人が63回目、750番目の人は134回目に当っていました。

このグラフを見ると、運が良い半数の人はそこそこスムーズに当たっていくものの、その後はどんどん回す回数が増え、運の悪い人は本当に何回回して当たらないものなんだなぁ……と感じました。

最後に、提供割合を倍の「2％」にした場合と、半分の「0.5％」にした場合のグラフを重ねて描いてみました。pyplot.hist()では「分布データのリスト」のリストを与えることで、複数のヒストグラムの重ね書きも簡単にできます。以下の例では、"counter"には提供割合1％の結果、"counter2"には2％の結果、"counter3"には0.5％の結果が入っています。

30  pyplot.hist([counter, counter2, counter3], bins=100, cumulative=True, histtype='step', label=['0.01', '0.02', '0.005'])
31  pyplot.axhline(int(player/4),ls='--',c='red')
32  pyplot.axhline(int(player/2), ls='--', c='red')
33  pyplot.axhline(int(player - player/4), ls='--', c='red')
34  pyplot.legend(loc='best')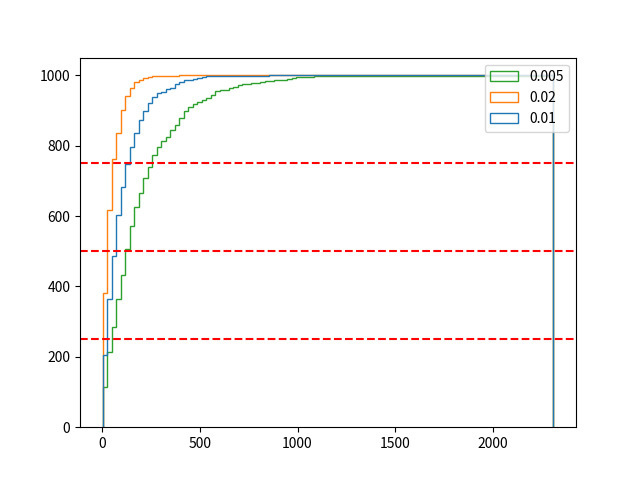

グラフの交点を調べると、提供割合2％の場合の四分位数はそれぞれ（14、27、53⁠）⁠、0.5％の場合の四分位数は（47、116、255）で、グラフからも見て取れるように、提供割合が半分（0.5％）になると、「⁠運の悪い人」が引けるまでにかかる回数は急激に増えて行き、1000番目の人は2300回回してようやく当たる、ということになりました。

さて、今回のシミュレーションでは「何回引けば何割の人が当たる」ことはわかったものの、果して自分が「運のいい側の1/4」（⁠＝30回以内に当たる）にいるのか「運の悪い側の1/4」（⁠＝100回以上引いても当たらない）にいるのかはわからず、当るまでにかかった回数から振り返って「運が（いい|悪い）側だった」と判断するしかありません。もっとも、第2四分位数（＝半数が当たる）を越えると当たるまでに回さないといけない回数は急速に増えていくので、提供割合が1％の場合、70回回して引けなかったら諦める、というのはひとつの基準になるかも知れません。

ネットの世界では、「⁠描けば出る」と称して狙っているキャラのイラストをtwitterやpixivに投稿したり、そのキャラと縁のある場所や物の近くでガチャを回したりする話をよく聞きます。「⁠科学的」な視点からは、その手の行為は「テルテル坊主に晴天を祈る」ような、いわゆる「類感呪術」の類いとして、非合理的な行為の典型例に見なされるでしょう。

一方、深層心理学を提唱したC.G.ユングは、「⁠易」や「占星術」の研究から、いわゆる「共時性（シンクロニシティ⁠）⁠」の概念を紹介し、「⁠虫の知らせ」のように、直接的な因果関係は存在しないものの、意味的な関連性を持つ事象が同時に発生しうることを主張しました。

ユングの言う「共時性」的な観点から見れば、確率を越えた「描けば出る」という現象もあり得ないわけではないものの、そのあたりをソフトウェア的に検証することは不可能なので、また別の機会に考えることにしましょう（笑。